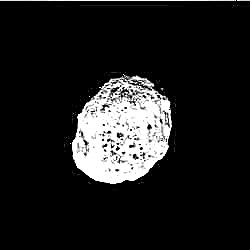
Ebben a képen a káoszelméletet demonstrálják, amelyet hosszú fény expozíciójával hoztak létre a kettős inga végén.
(Kép: © Wikimedia Commons / Cristian V.)
Nagyon jó lenne, ha nem csak egy héttel korábban, hanem egy hónappal vagy akár egy évvel a jövőben is tudnánk az időjárás-előrejelzést. Az időjárás előrejelzése azonban számos trükkös problémát jelent, amelyeket soha nem tudunk teljes mértékben megoldani. Az oka annak, hogy nemcsak a bonyolultság - a tudósok rendszeresen könnyedén foglalkoznak az összetett problémákkal - ez sokkal alapvető fontosságú. Ez a 20. század közepén fedezhető fel: az az igazság, hogy kaotikus univerzumban élünk, amely sok szempontból teljesen kiszámíthatatlan. De a káosz mélyén elrejtve meglepő minták vannak, olyan minták, amelyek ha valaha is képesek vagyunk megérteni őket, mélyebb kinyilatkoztatásokhoz vezethetnek.
A káosz megértése
A fizika egyik legszebb dolga az, hogy determinisztikus. Ha ismeri a rendszer összes tulajdonságát (ahol a "rendszer" bármit jelenthet egy dobozban lévő részecskéktől a Föld időjárási mintáinak vagy akár maga az univerzum fejlődésének), és ismeri a fizika törvényeit, akkor tökéletesen megjósolni a jövőt. Tudod, hogyan fog fejlődni a rendszer államokból az idő előrehaladtával. Ez a determinizmus. Ez lehetővé teszi a fizikusoknak, hogy előrejelzéseket készítsenek arról, hogy a részecskék, az időjárás és az egész világegyetem hogyan fog alakulni az idő múlásával.
Kiderül, hogy a természet determinisztikus és kiszámíthatatlan is lehet. Első útmutatást kaptunk az 1800-as években, amikor a svéd király mindenki számára díjat ajánlott fel, aki meg tudja oldani az úgynevezett három test problémáját. Ez a probléma a mozgás előrejelzésével foglalkozik Isaac Newton törvényei szerint. Ha a Naprendszer két tárgya csak a gravitáció révén kölcsönhatásba lép, akkor Newton törvényei pontosan megmondják, hogyan fog ez a két objektum jól viselkedni a jövőben. De ha hozzáad egy harmadik testet, és hagyja, hogy ez is játssza a gravitációs játékot, akkor nincs megoldás, és nem fogja tudni megjósolni a rendszer jövőjét.
Henri Poincaré (vitathatatlanul szuperhős) francia matematikus nyerte meg a díjat anélkül, hogy ténylegesen megoldotta volna a problémát. Megoldása helyett a problémáról írt, leírva minden okot, miért nem sikerült megoldani a problémát. Az egyik legfontosabb ok, amelyet kiemelt, az volt, hogy a rendszer elején kicsi különbségek miként vezetnek végül nagy különbségekhez.
Ezt az ötletet nagyrészt nyugtatni hagyták, és a fizikusok folytatták, feltételezve, hogy az univerzum determinisztikus. Vagyis a 20. század közepéig tették ezt, amikor Edward Lorenz matematikus egy korai számítógépen tanulmányozta a Föld időjárásának egyszerű modelljét. Amikor abbahagyta és újraindította a szimulációt, vadul eltérő eredményekkel járt, amelyeknek nem szabad dolognak lenniük. Pontosan ugyanazokat a bemeneteket adta be, és számítógépen oldotta meg a problémát, és a számítógépek igazán jók ugyanazt a dolgot újra és újra.
Amit meglepő érzékenységet talált a kezdeti körülményekkel szemben. Egy apró, legfeljebb 1 milliárd kerekítési hiba a modelljében az időjárás teljesen más viselkedéséhez vezetne.
Amit Lorenz alapvetően felfedezte, a káosz volt.
Botlás a sötétben
Ez egy kaotikus rendszer aláíró jele, amelyet Poincaré először azonosított. Általában, amikor egy rendszert nagyon alacsony változtatásokkal indít el a kezdeti körülmények között, akkor csak nagyon kicsi a változás a kimeneten. De az időjárással nem ez a helyzet. Egy apró változás (például egy pillangó Dél-Amerikában szárnyát lebegő) óriási különbséget okozhat az időjárásban (például egy új hurrikán kialakulása az Atlanti-óceánon).
A kaotikus rendszerek mindenhol vannak, sőt uralják az univerzumot. Ragassz egy ingot egy másik inga végére, és van egy nagyon egyszerű, de nagyon kaotikus rendszered. A három test problémája, amelyet Poincaré félreért, egy kaotikus rendszer. A faj populációja idővel kaotikus rendszer. A káosz mindenütt jelen van.
Ez a kezdeti körülményekre való érzékenység azt jelenti, hogy kaotikus rendszereknél lehetetlen határozott előrejelzéseket tenni, mivel soha nem tudhatja pontosan, pontosan, a végtelen tizedes pontig a rendszer állapotát. És ha még a legapróbb is van, elegendő idő eltelte után fogalmam sincs, mit csinál a rendszer.
Ezért lehetetlen tökéletesen megjósolni az időjárást.
A fraktálok titkai
Számos meglepő vonás van elfoglalva ebben a kiszámíthatatlanságban és a káoszban. Ezek elsősorban úgynevezett fázis térben jelennek meg, egy térképen, amely leírja a rendszer állapotát az egyes időpontokban. Ha ismeri a rendszer tulajdonságait egy adott pillanatfelvételnél, akkor leírhat egy pontot a fázis térben.
Ahogy a rendszer fejlődik, és megváltozik az állapota és tulajdonságai, elkészíthet egy új pillanatfelvételt és leírhat egy új pontot a fázis térben, idővel létrehozva a pontok gyűjteményét. Ha elegendő ilyen pont van, láthatja, hogyan viselkedett a rendszer az idő múlásával.
Néhány rendszer vonzerőknek nevezett mintát mutat. Ez azt jelenti, hogy függetlenül attól, hogy hol indítja el a rendszert, az végül egy olyan állapotba alakul ki, amelyet különösen szereti. Például, függetlenül attól, hogy hol dobja el a labdát a völgybe, a völgy végére kerül. Ez a rendszer vonzza a rendszert.
Amikor Lorenz megnézte egyszerű időjárási modelljének fázistérét, talált vonzót. De ez a vonzó nem hasonlított olyanra, mint amit korábban láttak. Időjárási rendszere rendszeres volt, de ugyanazt az állapotot soha nem ismételték meg kétszer. A fázis térben két pont sem volt átfedésben. Valaha.
Ellentmondás
Számos meglepő vonás van elfoglalva ebben a kiszámíthatatlanságban és a káoszban. Valaha.
Ez nyilvánvaló ellentmondásnak tűnt. Volt egy vonzó; azaz a rendszer előnyben részesített állapotkészletet választott. De ugyanaz az állapot soha nem ismétlődött meg. Ez a szerkezet csak fraktálként írható le.
Ha megnézi Lorenz egyszerű időjárási rendszerének fázistérét, és kicsit nagyít rá, látni fogja egy pontosan ugyanazon fázistér apró változatát. És ha elvesz egy kisebb részét és újra nagyítja, akkor látni fogja ugyanazon vonzerő finomabb verzióját. És így tovább és így tovább a végtelenig. A fraktálok olyan dolgok, amelyek minél közelebb néznek egymáshoz.
Tehát az időjárási rendszernek van vonzója, de ez furcsa. Ezért nevezik őket szó szerint furcsa vonzerőknek. És nemcsak időjárással, hanem mindenféle kaotikus rendszerben szaporodnak.
Nem értjük teljesen a furcsa vonzók természetét, azok jelentőségét, illetve azt, hogy miként használhatjuk őket kaotikus és kiszámíthatatlan rendszerekkel való együttműködéshez. Ez egy viszonylag új terület a matematika és a természettudomány területén, és még mindig megpróbáljuk a fejünket körültekerni. Lehetséges, hogy ezek a kaotikus rendszerek bizonyos értelemben determinisztikusak és kiszámíthatók. De ezt még nem kell kitalálni, tehát egyelőre csak be kell számolnunk a hétvégi időjárás-előrejelzésünkkel.
- Hogyan ideiglenesen szüntesse meg az univerzum végtelen káoszát kloroformmal
- A káosz jelei Űr háttérkép
- Forró káosz | Űr háttérkép
Paul M. Sutter asztrofizikus a Az Ohio Állami Egyetem, a "Kérdezz egy űrhajóstól" és "Space Radio, "és a"Helyed az univerzumban."
Tudjon meg többet az epizód meghallgatásával "Valóban kiszámítható az univerzum?" az „Ask a Spaceman” podcaston, amely elérhető az iTuneson és az interneten a http://www.askaspaceman.com címen.
Köszönet T. Carlos-nak, Akanksha B.-nek, @TSFoundtainworks-nek és Joyce-nak S.-nak a kérdésért, amely a darabhoz vezetett! Tegye fel saját kérdését a Twitteren a #AskASpaceman segítségével, vagy Paul @PaulMattSutter és facebook.com/PaulMattSutter követésével.