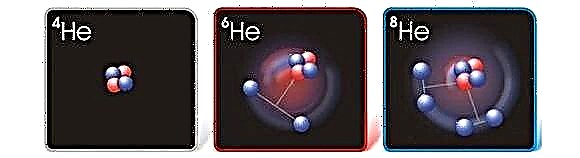
Egy repülőgép Marsra építése jelentős előnyei lennének a felület felderítésének. Ez a föld tengerszintjének sűrűségének csak 1,6% -a, adj vagy vegyen. Ez azt jelenti, hogy a hagyományos repülőgépeknek nagyon gyorsan repülniük kell a Marson, hogy alul maradjanak. Az átlagos Cessna bajban lesz.
De a természet alternatív módon kínálhatja ezt a problémát.
Bármely repülõ (vagy úszó) állat, gép stb. Folyadékáramát Reynolds-számnak (Re) nevezzük. A Re egyenlő a karakterisztikus hossz x sebesség x folyadék sűrűsége osztva a dinamikus viszkozitással. Ez a tehetetlenség és a viszkózus erők arányának mértéke. Átlagos repülőgépe magas Re: sok inerciával repül a levegő tapadásához viszonyítva. Mivel a Mars levegõ sûrûsége alacsony, ezt a tehetetlenséget csak azért lehet elérni, ha nagyon gyorsan megyünk. Ugyanakkor nem minden szórólap működik magas Re mellett: a legtöbb repülő állat sokkal alacsonyabb Re mellett repül. Különösen a rovarok működnek meglehetősen kis Reynolds-számokon (viszonylag szólva). Valójában néhány rovar olyan kicsi, hogy a levegőben úszik, nem pedig repül. Tehát, ha csak egy kicsit méretezünk fel egy hibás-szerű botrányt vagy kisméretű madarat, akkor kaphatunk valamit, ami képes mozogni a marsi légkörben anélkül, hogy őrülten gyorsan el kellene mennie.
Szükségünk van egy egyenletrendszerre a kis robotunk korlátozására. Kiderült, hogy ez nem túl nehéz. Durva közelítésként használhatjuk Colin Pennycuick átlagos csapkodási frekvencia egyenletét. A Pennycuick (2008) villámlásfrekvencia-elvárásai alapján a csapkodási frekvencia nagyjából változik: testtömeg a 3/8 teljesítményig, gravitációs gyorsulás az 1/2 teljesítményig, a –23/24 teljesítményig, a szárny terület -1-ig / 3 teljesítmény és folyadék sűrűsége a -3/8 teljesítményig. Ez nagyon hasznos, mert beállíthatjuk a marsi gravitációt és a levegő sűrűségét. De tudnunk kell, hogy ésszerű módon forgácsolunk-e örvényeket a szárnyakból. Szerencsére ott is ismert kapcsolat van: a Strouhal-szám. Str (ebben az esetben) a csapkodási amplitúdó x csapkodási frekvencia osztva a sebességgel. Hajózás közben nagyon korlátozottnak bizonyul.
Ezért botunknak 0,2 és 0,4 közötti Str értékűnek kell lennie, miközben megegyezik a Pennycuick egyenlettel. És végül, be kell szereznünk egy Reynolds-számot a nagy élő élő rovarok tartományába (apró rovarok furcsa üzemmódban repülnek, ahol a hajtóerő nagy része húzódáson alapszik, tehát egyelőre ezeket figyelmen kívül hagyjuk). A Hawkmoth-ot jól tanulmányozták, tehát a különböző sebességekre rendelkezésre áll a Re tartomány. A sebességetől függően körülbelül 3500 és körülbelül 15 000 között mozog. Tehát valahol a gördülőparkban meg fog csinálni.
A rendszer megoldásának néhány módja van. Az elegáns módszer a görbék generálása és a keresztezési pontok keresése, ám gyors és egyszerű módszer az, hogy lyukasztják be egy mátrix programba, és iteratívan oldják meg. Nem adom meg az összes lehetséges lehetőséget, de itt van egy, amely nagyon jól működött, hogy ötletet adjon:
Tömeg: 500 gramm
Span: 1 méter
Szárnyméretarány: 8,0
Ez 0,31 Str-t (közvetlenül a pénznél) és Re = 13 900-t (tisztességes) ad 0,5 emelési együtthatóval (ami ésszerű a hajózáshoz). Ötletet adva ennek a botnak nagyjából madárszerű arányai lennének (hasonlóan a kacsához), bár kissé a könnyű oldalon (nem kemény jó szintetikus anyagokkal). Ugyanakkor nagyobb ívben áthaladna magasabb frekvencián, mint egy madár itt a Földön, tehát kissé úgy néz ki, mint egy óriás lepke, távolságban a Föld által kiképzett szemünktől. Kiegészítő bónuszként, mivel ez a bot egy molyhos Reynolds-rendszerben repül, valószínű, hogy bizonytalan dinamika segítségével átmenetileg képes a rovarok nagyon magas emelési tényezőire való áttéréshez rövid ideig. A 4.0 CL-nál (amelyet apró denevéreknek és légykapóknak, valamint néhány nagy méhnek is mértek) az elakadási sebesség csak 19,24 m / s. A Max CL a leghasznosabb a leszálláshoz és az induláshoz. Tehát: indíthatunk-e botot 19,24 m / s sebességgel?
Tegyük fel, hogy a móka kedvéért tegyük fel, hogy a madár- / bugbotunk is úgy indul el, mint egy állat. Az állatok nem szállnak fel, mint a repülőgépek; ballisztikus iniciációt használnak az aljzatból történő kitolással. A rovarok és a madarak sétáló végtagokat használnak erre, de a denevérek (és valószínűleg pterozauruszok) a szárnyak megduplázására szolgálnak tolórendszerként. Ha robotjainkat szárnyasra tettük, akkor ugyanazt a motort használhatjuk felindításra, mint repülésre, és kiderül, hogy nincs szükség nagy nyomásra. Az alacsony Mars-gravitációnak köszönhetően még egy kis ugrás is messzire megy, és a szárnyak már 19,24 m / s közelében is vertek, amint van. Tehát csak egy kis komló fog megcsinálni. Ha divatosnak érezzük magunkat, egy kicsit több ütést tehetünk rá, és ez kikerül a kráterekből stb. Akárhogy is, botunknak csak kb. 4% -ának kell lennie olyan hatékonynak, mint egy jó ugrónak, mint a jó biológiai jumpereknek. fel a sebességre.
Ezek a számok természetesen csak durva szemléltetést jelentenek. Sok oka van annak, hogy az űrprogramok még nem indítottak ilyen típusú robotokat. A telepítés, az energiaellátás és a karbantartás problémái e rendszerek hatékony kihasználását nagyon nehézségekbe ütköztetik, de lehet, hogy nem teljesen lehetetlen. Lehet, hogy egy nap roverjeink kacsaméretű lepkebottokat fognak telepíteni a többi világ jobb megismerése érdekében.